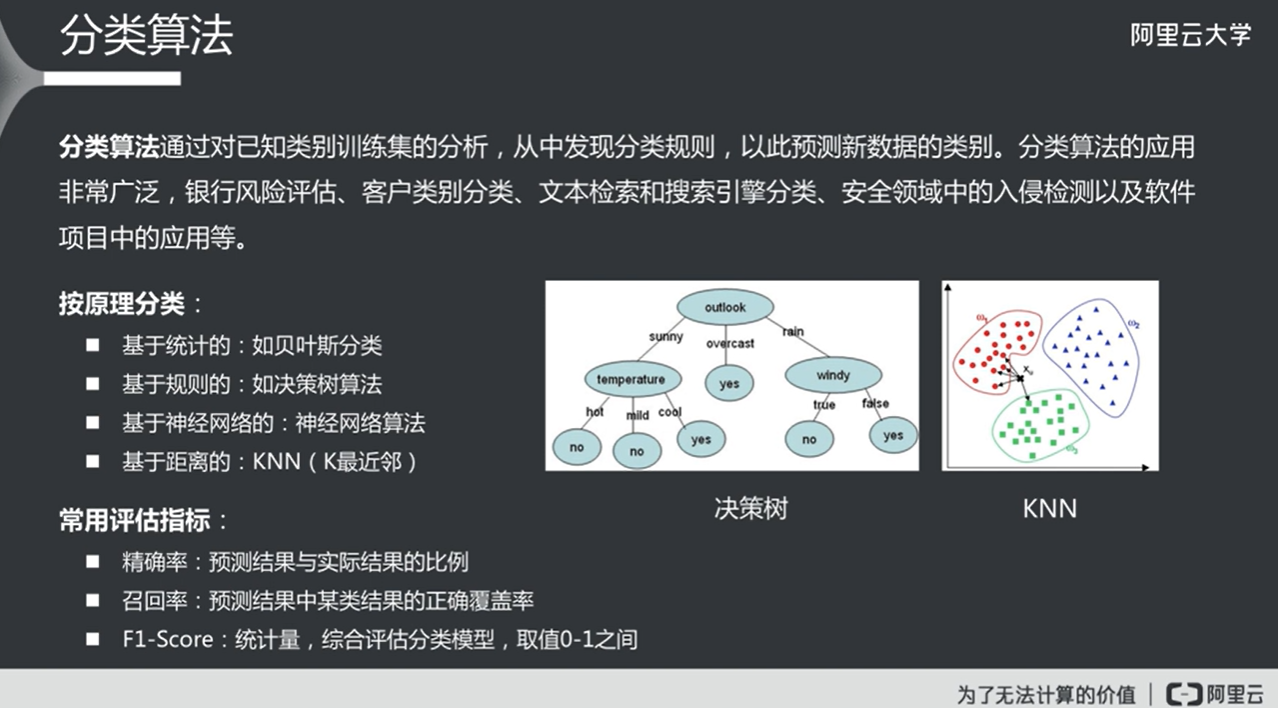
机器学习入门 1.常见算法 有监督学习算法
分类(Classification)
回归(Regression)
knn 根据当前样本跟其他样本的距离来对当前样本进行分类,超参数k用于圈定范围
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 KNN(K-Nearest Neighbors,K最近邻)是一种简单而有效的监督学习算法,广泛用于分类和回归任务。KNN 的基本思想是通过计算样本之间的距离来进行预测,具体步骤如下: ### 基本原理 1. **训练阶段**: - KNN 是一种懒惰学习(lazy learning)算法,它在训练阶段并不构建显式的模型,而是简单地存储训练数据。 2. **预测阶段**: - 对于一个新的输入样本,KNN 会计算该样本与训练集中所有样本的距离(通常使用欧几里得距离、曼哈顿距离等)。 - 找到距离最近的 K 个邻居。 - 对于分类任务,KNN 会根据这 K 个邻居的类别进行投票,选择出现次数最多的类别作为预测结果。 - 对于回归任务,KNN 会计算这 K 个邻居的平均值作为预测结果。 ### 选择 K 值 - K 值的选择对 KNN 的性能有很大影响: - **小的 K 值**(如 K=1)可能导致模型对噪声敏感,容易过拟合。 - **大的 K 值**可能导致模型过于平滑,无法捕捉到数据的局部结构,容易欠拟合。 - 通常通过交叉验证来选择最佳的 K 值。 ### 距离度量 KNN 依赖于距离度量来判断邻居的“近”与“远”。常用的距离度量包括: - **欧几里得距离**:最常用的距离度量,适用于连续特征。 - **曼哈顿距离**:适用于某些特定场景,计算方式为各维度差值的绝对值之和。 - **闵可夫斯基距离**:是欧几里得距离和曼哈顿距离的推广。 - **余弦相似度**:适用于文本数据等高维稀疏数据。 ### 优缺点 #### 优点: - 简单易懂,易于实现。 - 不需要假设数据的分布。 - 可以用于多分类问题。 #### 缺点: - 计算复杂度高:在预测时需要计算所有训练样本的距离,随着数据量的增加,计算时间会显著增加。 - 存储复杂度高:需要存储所有训练样本。 - 对于高维数据,KNN 的性能可能下降(维度灾难)。 ### 应用场景 KNN 被广泛应用于各种领域,包括但不限于: - 图像识别 - 文本分类 - 推荐系统 - 医疗诊断 ### 示例代码 以下是一个使用 Python 和 `scikit-learn` 库实现 KNN 分类的简单示例: ```python import numpy as np from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score # 加载数据集 iris = load_iris() X = iris.data y = iris.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建 KNN 分类器 k = 3 knn = KNeighborsClassifier(n_neighbors=k) # 训练模型 knn.fit(X_train, y_train) # 进行预测 y_pred = knn.predict(X_test) # 计算准确率 accuracy = accuracy_score(y_test, y_pred) print(f'Accuracy: {accuracy:.2f}') ``` 这个示例中,我们使用了鸢尾花数据集(Iris dataset),将数据集划分为训练集和测试集,创建了一个 KNN 分类器,并计算了模型的准确率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 在 KNN(K-Nearest Neighbors)算法中,分类的过程是基于已有的训练数据进行的。对于第一个样本(即在训练集中的第一个样本),它的类别是由训练数据本身决定的,而不是通过 KNN 算法来推断的。以下是详细的解释: ### 1. 训练阶段 在 KNN 的训练阶段,算法并不进行任何模型的构建或参数的学习。相反,它只是将训练数据存储在内存中。每个样本都有一个已知的类别标签,这些标签是在数据收集时就已经确定的。 ### 2. 第一个样本的类别 - **已知类别**:在训练数据集中,每个样本都有一个对应的类别标签。第一个样本的类别是数据集中预先定义的,通常是在数据收集和标注阶段就已经确定的。 - **存储**:KNN 仅仅是将这些样本及其对应的类别存储起来,以便在预测阶段使用。 ### 3. 预测阶段 当 KNN 接收到一个新的样本进行分类时,它会执行以下步骤: 1. **计算距离**:计算新样本与训练集中所有样本的距离。 2. **选择 K 个邻居**:找到距离新样本最近的 K 个训练样本。 3. **投票**:根据这 K 个邻居的类别进行投票,选择出现次数最多的类别作为新样本的预测类别。 ### 例子 假设我们有一个简单的训练集: | 样本 | 特征1 | 特征2 | 类别 | |------|-------|-------|------| | 1 | 2.0 | 3.0 | A | | 2 | 1.0 | 1.0 | B | | 3 | 4.0 | 5.0 | A | | 4 | 5.0 | 4.0 | B | 在这个例子中,样本 1 的类别是 A,样本 2 的类别是 B,样本 3 的类别是 A,样本 4 的类别是 B。这些类别是在训练数据准备阶段就已经确定的。 当我们要对一个新的样本(例如,特征为 (3.0, 3.0))进行分类时,KNN 会计算这个新样本与训练集中所有样本的距离,找到最近的 K 个邻居,然后根据这些邻居的类别进行投票,最终确定新样本的类别。 ### 总结 KNN 算法的核心在于利用已有的训练数据进行分类,而不是通过算法推断第一个样本的类别。每个样本的类别是在数据准备阶段就已经确定的,KNN 仅仅是利用这些已知的类别进行预测。
决策树 信息熵
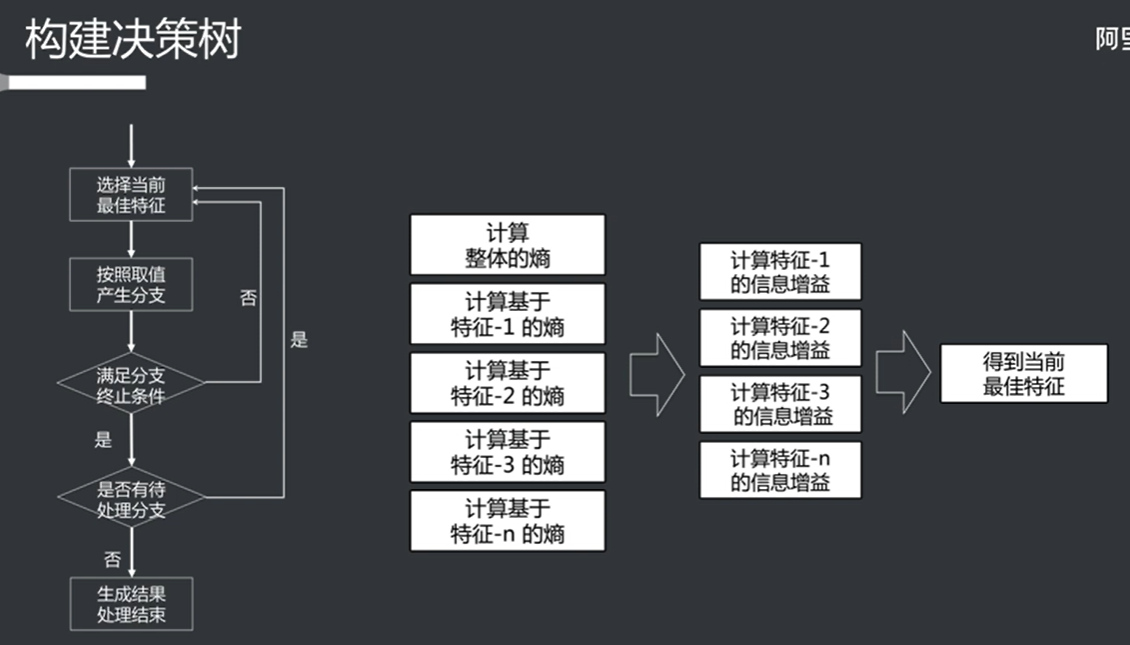
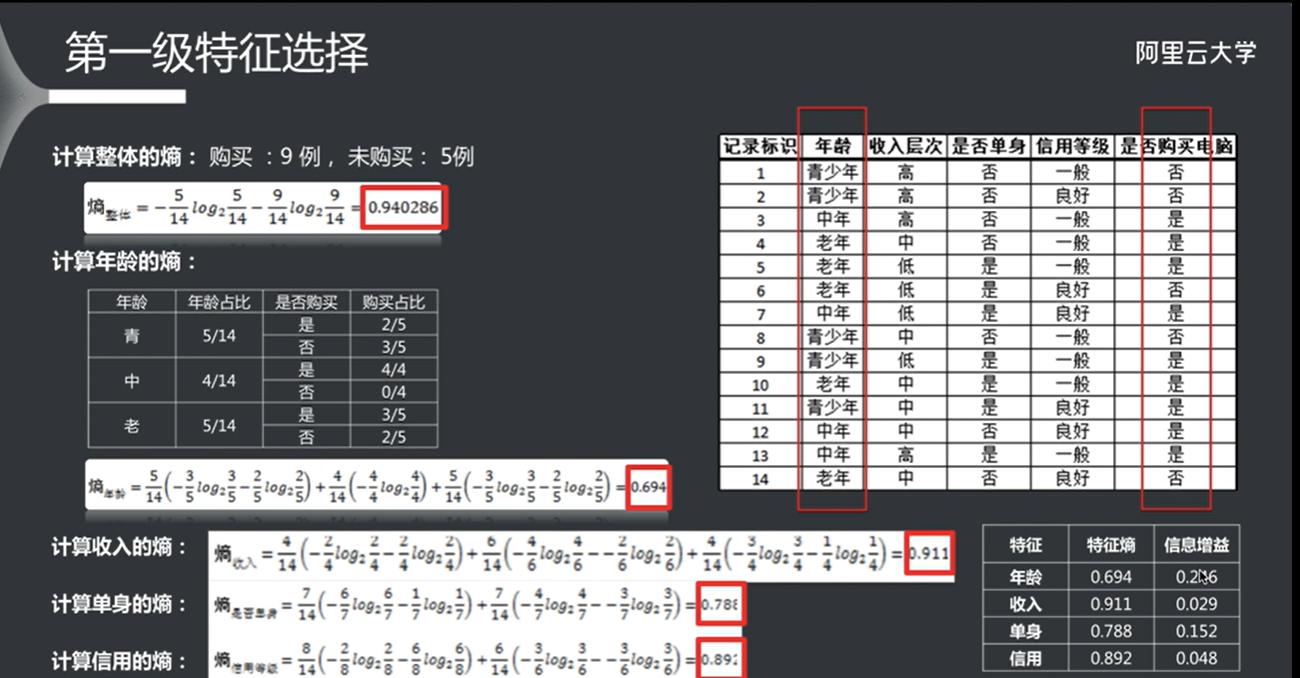
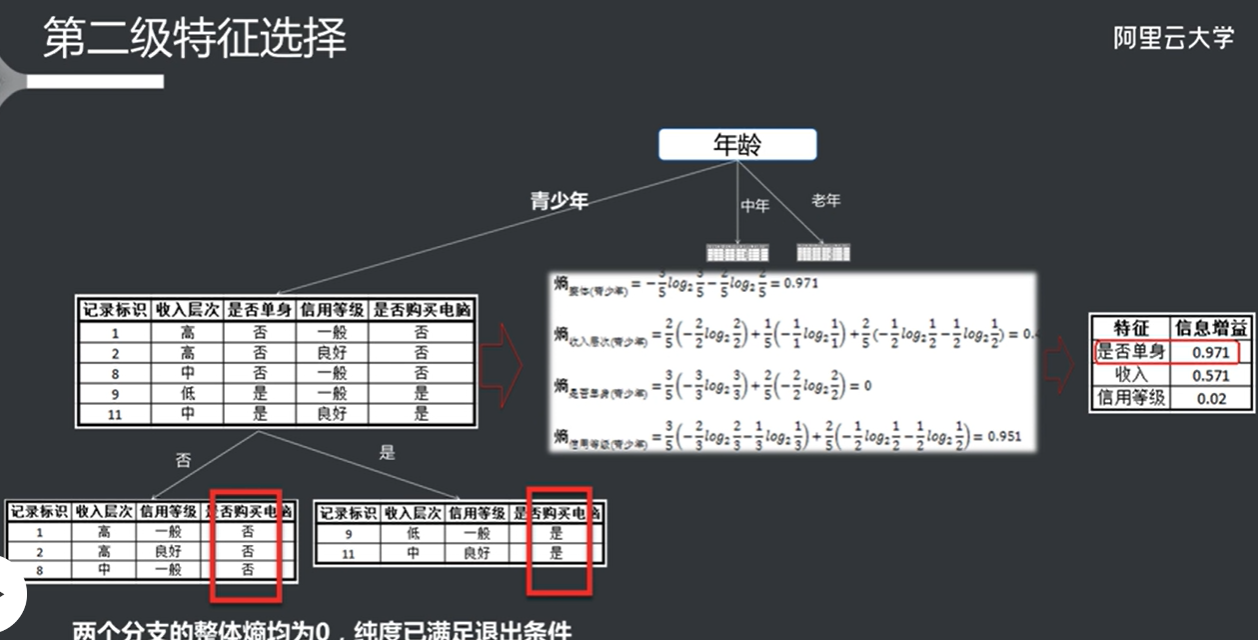
信息增益和特征选择 其实就是通过某个属性对熵的减弱(也就是信息增益的大小),如果信息增益比较强的话,就以这个属性作为特征。
可以理解为认识一个事物的过程就是提取特征然后下定义的过程,如此就可以以这个属性作为机器学习中的有效特征。(权重比较强的,大概是这样)
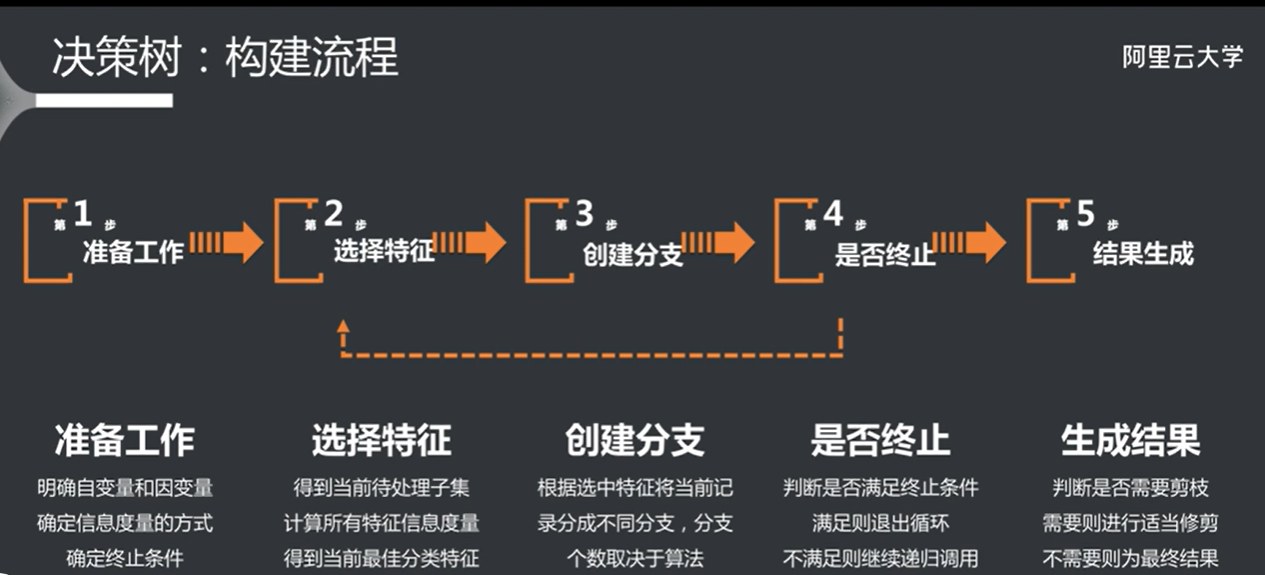
根据信息增益,将每个属性的权重计算出来,其实就是得到最佳特征的过程。
选择完第一个特征之后根据特征进行分支,然后再选出第二个特征,以此类推。
根据循环的停止条件来判断是否继续分支(如纯度,循环次数等)
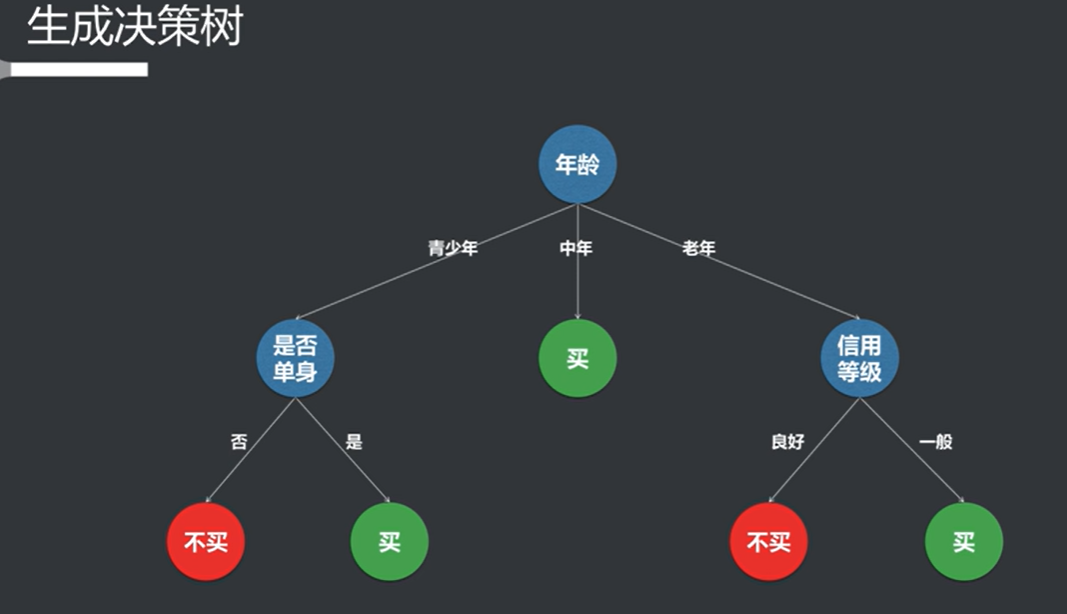
全部停止之后生成决策树
基尼系数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 基尼系数(Gini Coefficient)是一个用于衡量收入或财富分配不平等程度的统计指标。它由意大利统计学家科拉多·基尼(Corrado Gini)于 1912 年提出。基尼系数的值范围从 0 到 1,或者可以表示为 0% 到 100%。以下是基尼系数的详细介绍: ### 1. 基尼系数的定义 - **完全平等**:如果一个国家或地区的收入分配完全平等,所有人都有相同的收入,则基尼系数为 0。 - **完全不平等**:如果一个国家或地区的收入分配完全不平等,所有收入都集中在一个人手中,其余人没有收入,则基尼系数为 1。 ### 2. 计算方法 基尼系数可以通过洛伦兹曲线(Lorenz Curve)来计算。洛伦兹曲线是一个图形,表示收入分配的累积比例。基尼系数可以通过以下公式计算: \[ G = \frac{A}{A + B} \] 其中: - \(A\) 是洛伦兹曲线与完全平等线之间的面积。 - \(B\) 是洛伦兹曲线下方的面积。 基尼系数也可以通过以下公式计算: \[ G = 1 - 2 \int_0^1 L(p) \, dp \] 其中 \(L(p)\) 是洛伦兹曲线的函数,\(p\) 是收入的累积比例。 ### 3. 基尼系数的解释 - **基尼系数为 0**:表示完全平等,所有人收入相同。 - **基尼系数为 0.2**(或 20%):表示收入分配相对平等。 - **基尼系数为 0.5**(或 50%):表示收入分配不平等。 - **基尼系数为 1**(或 100%):表示完全不平等,所有收入集中在一个人手中。 ### 4. 应用 基尼系数广泛应用于经济学、社会学和公共政策等领域,主要用于: - 衡量国家或地区的收入不平等程度。 - 评估政策对收入分配的影响。 - 比较不同国家或地区的收入分配状况。 ### 5. 优缺点 #### 优点: - **简单易懂**:基尼系数的计算和解释相对简单。 - **广泛适用**:可以用于不同国家、地区和时间段的比较。 #### 缺点: - **信息损失**:基尼系数只提供了收入分配的一个总体指标,可能忽略了分配的具体情况。 - **不敏感于极端值**:基尼系数对极端收入的变化不够敏感,可能无法反映收入分配的真实情况。 ### 总结 基尼系数是一个重要的经济指标,用于衡量收入或财富分配的不平等程度。通过基尼系数,政策制定者和研究人员可以更好地理解和分析社会经济问题,制定相应的政策来改善收入分配状况。
决策树停止条件 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 在构建决策树时,停止分支的条件是非常重要的,因为它直接影响到模型的复杂性和泛化能力。以下是一些常见的停止分支条件: ### 1. **达到最大深度** - **最大深度限制**:设置一个最大深度参数,限制决策树的深度。当树的深度达到这个限制时,停止进一步分支。这有助于防止过拟合。 ### 2. **最小样本数** - **最小样本数限制**:在某个节点上,如果样本数少于设定的最小样本数(如 `min_samples_split`),则停止分支。这可以防止在样本数量非常少的情况下进行分支,从而减少过拟合的风险。 ### 3. **信息增益或基尼指数的阈值** - **信息增益阈值**:如果在某个节点上进行分支所获得的信息增益小于设定的阈值,则停止分支。信息增益越小,表示该特征对分类的贡献越小。 - **基尼指数阈值**:类似地,如果基尼指数的减少小于某个阈值,也可以停止分支。 ### 4. **纯度阈值** - **节点纯度**:如果某个节点的样本已经完全属于同一类别(即节点的纯度达到 100%),则停止分支。此时,节点可以被标记为叶子节点。 ### 5. **达到预设的叶子节点数量** - **叶子节点数量限制**:可以设置一个最大叶子节点数量,当达到这个数量时,停止分支。这有助于控制模型的复杂性。 ### 6. **交叉验证** - **交叉验证**:在训练过程中,可以使用交叉验证来评估模型的性能。如果进一步分支导致验证集的性能下降,则可以停止分支。 ### 7. **其他启发式方法** - **启发式方法**:有时可以使用其他启发式方法来决定是否停止分支,例如基于领域知识或经验法则。 ### 总结 决策树的停止分支条件可以通过多种方式来设定,通常是结合多种条件来确保模型的有效性和泛化能力。合理的停止条件可以帮助避免过拟合,提高模型在未见数据上的表现。
生成决策树算法
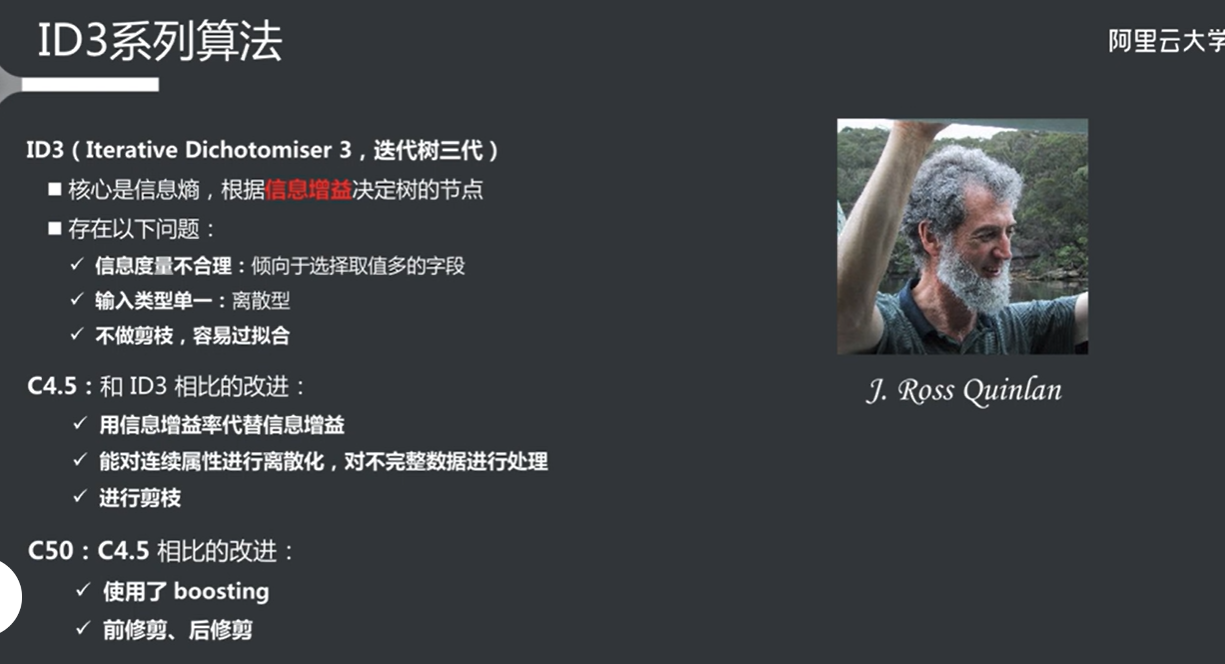
id3系列算法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 ID3(Iterative Dichotomiser 3)是一种用于构建决策树的算法,由 Ross Quinlan 在 1986 年提出。ID3 算法是基于信息增益的,主要用于分类任务。ID3 算法的基本思想是通过选择最能区分样本的特征来构建决策树。ID3 算法的后续版本和相关算法包括 C4.5 和 C5.0。以下是这些算法的简要介绍: ### 1. ID3 算法 - **基本原理**:ID3 使用信息增益作为特征选择的标准。信息增益衡量的是通过选择某个特征来减少的不确定性。 - **构建过程**: 1. 计算每个特征的信息增益。 2. 选择信息增益最大的特征作为当前节点的分裂特征。 3. 根据该特征的不同取值划分数据集。 4. 对每个子集递归地重复上述过程,直到满足停止条件(如达到最大深度、样本数不足等)。 - **优缺点**: - 优点:简单易懂,易于实现。 - 缺点:容易过拟合,特别是在特征较多时;对噪声敏感。 ### 2. C4.5 算法 C4.5 是 ID3 的改进版本,由 Ross Quinlan 在 1993 年提出。它在 ID3 的基础上进行了多项改进: - **使用增益比**:C4.5 使用增益比(Gain Ratio)而不是信息增益来选择特征。增益比考虑了特征的取值数量,避免了 ID3 偏向于选择取值较多的特征的问题。 \[ \text{Gain Ratio} = \frac{\text{Information Gain}}{\text{Split Information}} \] - **处理连续特征**:C4.5 可以处理连续特征,通过选择合适的阈值将其离散化。 - **处理缺失值**:C4.5 可以处理缺失值,通过将缺失值视为一个额外的类别或通过加权来处理。 - **剪枝**:C4.5 引入了剪枝技术,以减少过拟合。剪枝是在树构建完成后,通过移除一些不必要的节点来简化树结构。 ### 3. C5.0 算法 C5.0 是 C4.5 的进一步改进版本,具有以下特点: - **更高的效率**:C5.0 在构建决策树时比 C4.5 更快,尤其是在处理大数据集时。 - **更好的准确性**:C5.0 在分类准确性上通常优于 C4.5。 - **Boosting**:C5.0 支持 Boosting 技术,可以通过组合多个弱分类器来提高模型的性能。 - **更好的内存管理**:C5.0 在内存使用上进行了优化,适合处理大规模数据集。 ### 总结 ID3、C4.5 和 C5.0 是决策树算法的经典代表。ID3 是最早的版本,主要使用信息增益进行特征选择;C4.5 改进了 ID3,使用增益比并引入了处理连续特征和缺失值的能力;C5.0 则在效率和准确性上进一步提升,并引入了 Boosting 技术。决策树算法因其直观性和易于解释的特性,在许多领域得到了广泛应用。
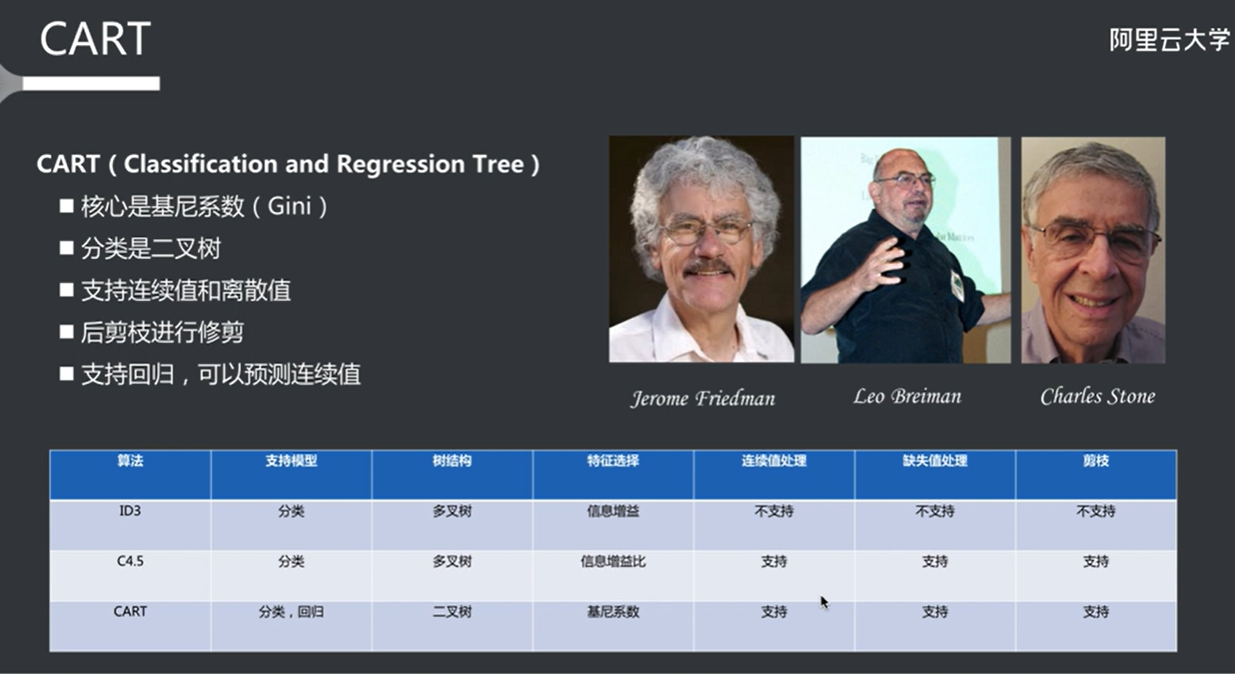
cart算法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 CART(Classification and Regression Trees)是一种用于分类和回归的决策树算法,由 Breiman 等人在 1986 年提出。CART 是一种非常灵活的算法,能够处理各种类型的数据,并且在许多机器学习任务中得到了广泛应用。以下是 CART 算法的主要特点和工作原理: ### 1. 基本原理 CART 可以用于两种主要任务: - **分类**:用于分类任务,输出类别标签。 - **回归**:用于回归任务,输出连续值。 ### 2. 特征选择 CART 在构建决策树时,使用不同的标准来选择特征: - **分类任务**:CART 使用基尼指数(Gini Index)作为特征选择的标准。基尼指数衡量的是一个节点的不纯度,计算公式为: \[ Gini(D) = 1 - \sum_{i=1}^{C} p_i^2 \] 其中 \(p_i\) 是类别 \(i\) 在数据集 \(D\) 中的比例,\(C\) 是类别的总数。CART 会选择使基尼指数最小化的特征进行分裂。 - **回归任务**:CART 使用均方误差(Mean Squared Error, MSE)作为特征选择的标准。均方误差计算公式为: \[ MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - \bar{y})^2 \] 其中 \(y_i\) 是实际值,\(\bar{y}\) 是预测值。CART 会选择使均方误差最小化的特征进行分裂。 ### 3. 树的构建 CART 的树构建过程如下: 1. **选择特征**:计算所有特征的基尼指数(分类)或均方误差(回归),选择最优特征进行分裂。 2. **分裂节点**:根据选择的特征和最佳阈值将数据集分成两个子集。 3. **递归构建**:对每个子集递归地重复上述过程,直到满足停止条件(如达到最大深度、样本数不足、节点纯度达到 100% 等)。 4. **生成叶子节点**:当停止条件满足时,生成叶子节点,并为其分配类别标签(分类)或预测值(回归)。 ### 4. 剪枝 CART 算法通常会在树构建完成后进行剪枝,以减少过拟合。剪枝的过程包括: - **预剪枝**:在树构建过程中,设置一些条件(如最小样本数、最大深度等),在满足条件时停止分裂。 - **后剪枝**:在树构建完成后,评估每个节点的贡献,移除一些不必要的节点,以简化树结构。 ### 5. 优缺点 #### 优点: - **灵活性**:CART 可以处理分类和回归问题。 - **易于解释**:决策树的结构直观,易于理解和解释。 - **处理缺失值**:CART 可以处理缺失值,具有一定的鲁棒性。 #### 缺点: - **过拟合**:CART 容易在训练数据上过拟合,尤其是在数据量较小或特征较多时。 - **不稳定性**:小的变化可能导致树结构的显著变化。 ### 总结 CART 是一种强大的决策树算法,能够处理分类和回归任务。通过使用基尼指数和均方误差作为特征选择标准,CART 能够有效地构建决策树。剪枝技术的引入有助于提高模型的泛化能力。CART 算法在许多实际应用中得到了广泛的应用,包括金融、医疗、市场营销等领域。
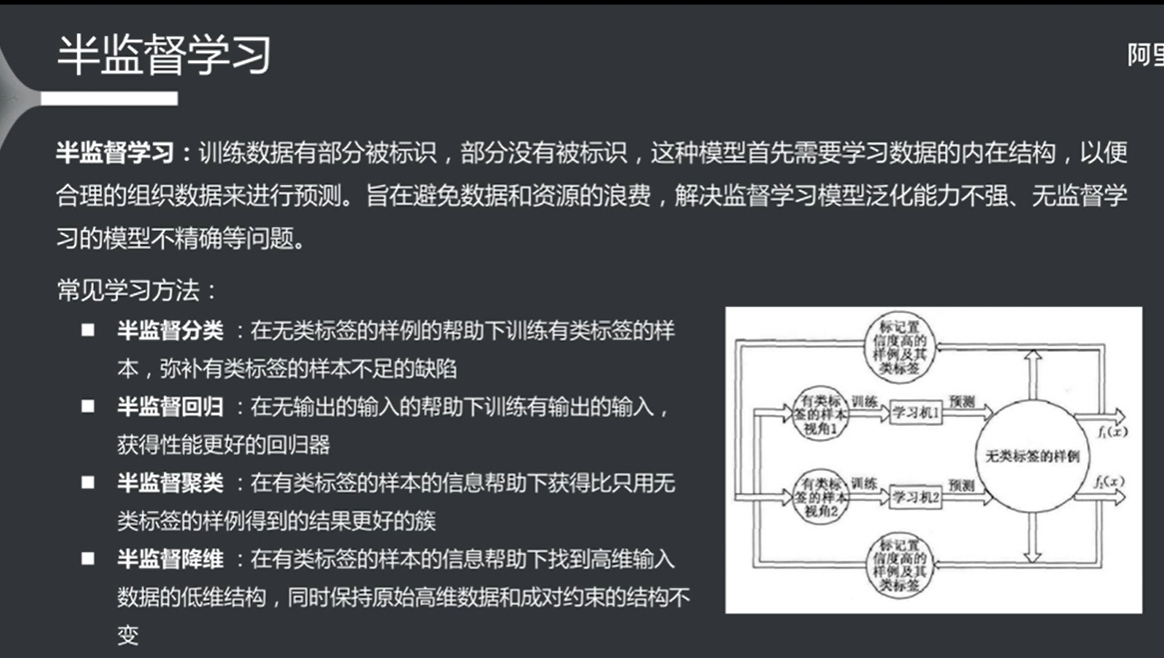
无监督学习算法 没有给出结论的样本数据
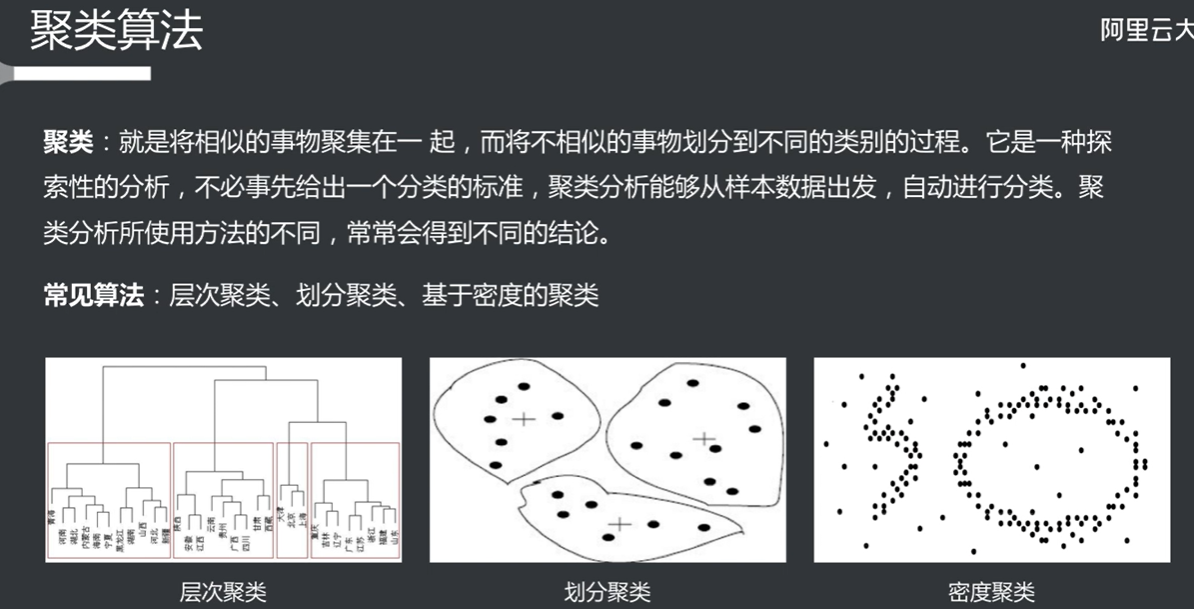
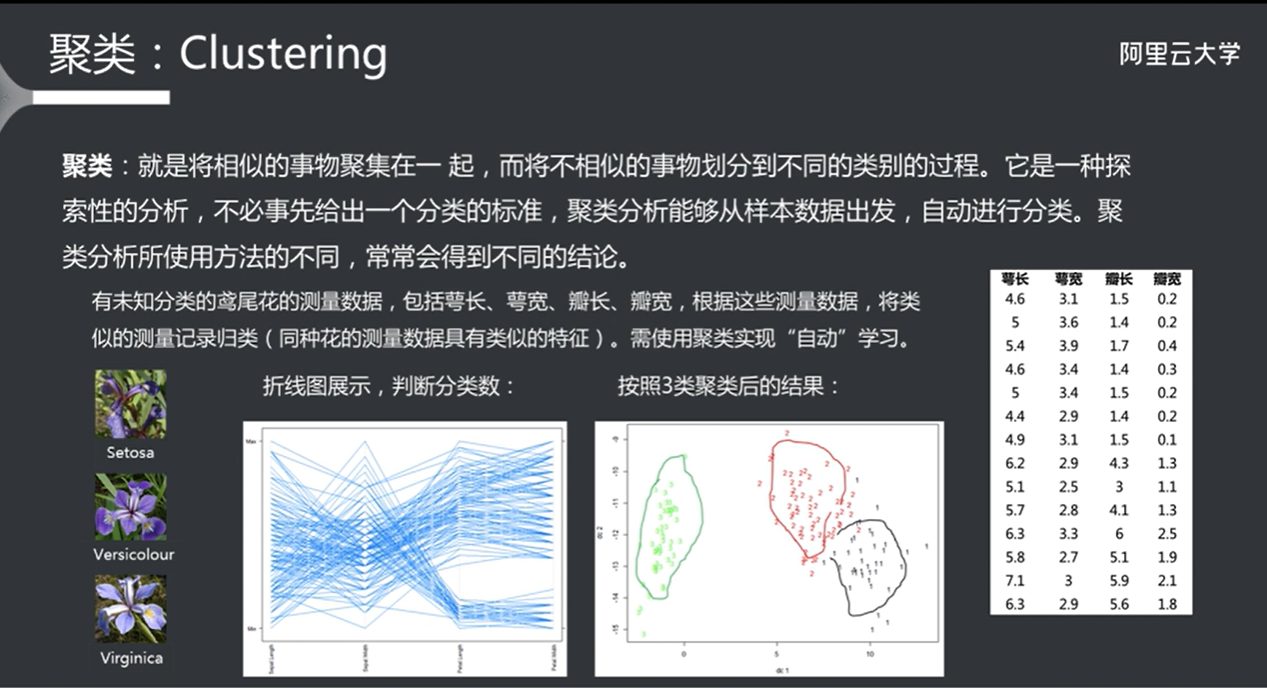
聚类算法
K-Means算法 超参数k为中心的个数(k的个数对结果的影响很大)
不断迭代计算出类的中心,直到类的中心不再变化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 K-means 算法是一种广泛使用的聚类算法,旨在将数据集分成 K 个簇(clusters),使得同一簇内的数据点尽可能相似,而不同簇之间的数据点尽可能不同。K-means 算法简单易懂,计算效率高,适用于大规模数据集。以下是 K-means 算法的详细介绍: ### 1. 算法原理 K-means 算法的基本步骤如下: 1. **选择 K 值**:确定要将数据集分成多少个簇(K 的值)。 2. **初始化中心**:随机选择 K 个数据点作为初始簇中心(centroids)。 3. **分配簇**: - 对于数据集中的每个数据点,计算其与 K 个簇中心的距离(通常使用欧几里得距离)。 - 将每个数据点分配给距离最近的簇中心。 4. **更新中心**: - 重新计算每个簇的中心,方法是计算分配给该簇的所有数据点的均值。 5. **重复步骤 3 和 4**:直到簇中心不再发生变化(收敛)或达到预设的迭代次数。 ### 2. 算法的数学表示 - **距离计算**:对于数据点 \(x_i\) 和簇中心 \(c_k\),使用欧几里得距离计算: \[ d(x_i, c_k) = \sqrt{\sum_{j=1}^{n} (x_{ij} - c_{kj})^2} \] - **簇中心更新**:对于簇 \(C_k\) 中的所有数据点 \(x_i\),簇中心 \(c_k\) 更新为: \[ c_k = \frac{1}{|C_k|} \sum_{x_i \in C_k} x_i \] ### 3. K-means 的优缺点 #### 优点: - **简单易懂**:K-means 算法易于实现和理解。 - **高效**:对于大规模数据集,K-means 算法的计算效率较高,时间复杂度为 \(O(n \cdot k \cdot i)\),其中 \(n\) 是数据点数量,\(k\) 是簇的数量,\(i\) 是迭代次数。 - **可扩展性**:适用于大规模数据集。 #### 缺点: - **K 值的选择**:需要事先指定 K 值,选择不当可能导致聚类效果不佳。 - **对初始值敏感**:不同的初始簇中心可能导致不同的聚类结果,可能会陷入局部最优解。 - **对噪声和离群点敏感**:K-means 对噪声和离群点敏感,可能影响聚类结果。 - **假设簇是球形的**:K-means 假设簇是球形的,且各簇的大小相似,这在某些情况下可能不成立。 ### 4. K-means 的改进 为了克服 K-means 的一些缺点,研究人员提出了一些改进算法,例如: - **K-means++**:一种改进的初始化方法,通过选择更远离已有簇中心的点作为初始中心,减少对初始值的敏感性。 - **层次聚类**:结合 K-means 和层次聚类的方法,先进行层次聚类,再使用 K-means 进行细化。 - **DBSCAN**:一种基于密度的聚类算法,能够识别任意形状的簇,并且对噪声和离群点具有更好的鲁棒性。 ### 5. 应用场景 K-means 算法广泛应用于多个领域,包括但不限于: - 图像压缩 - 市场细分 - 社交网络分析 - 文本聚类 - 生物信息学 ### 示例代码 以下是一个使用 Python 和 `scikit-learn` 库实现 K-means 聚类的简单示例: ```python import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_blobs from sklearn.cluster import KMeans # 生成示例数据 X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0) # 创建 K-means 模型 kmeans = KMeans(n_clusters=4) kmeans.fit(X) # 获取聚类结果 y_kmeans = kmeans.predict(X) # 可视化结果 plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis') centers = kmeans.cluster_centers_ plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X') plt.title('K-means Clustering') plt.show() ``` 在这个示例中,我们生成了一个包含 300 个样本的示例数据集,并使用 K-means 算法将其聚类为 4 个簇。最后,我们可视化了聚类结果和簇中心。
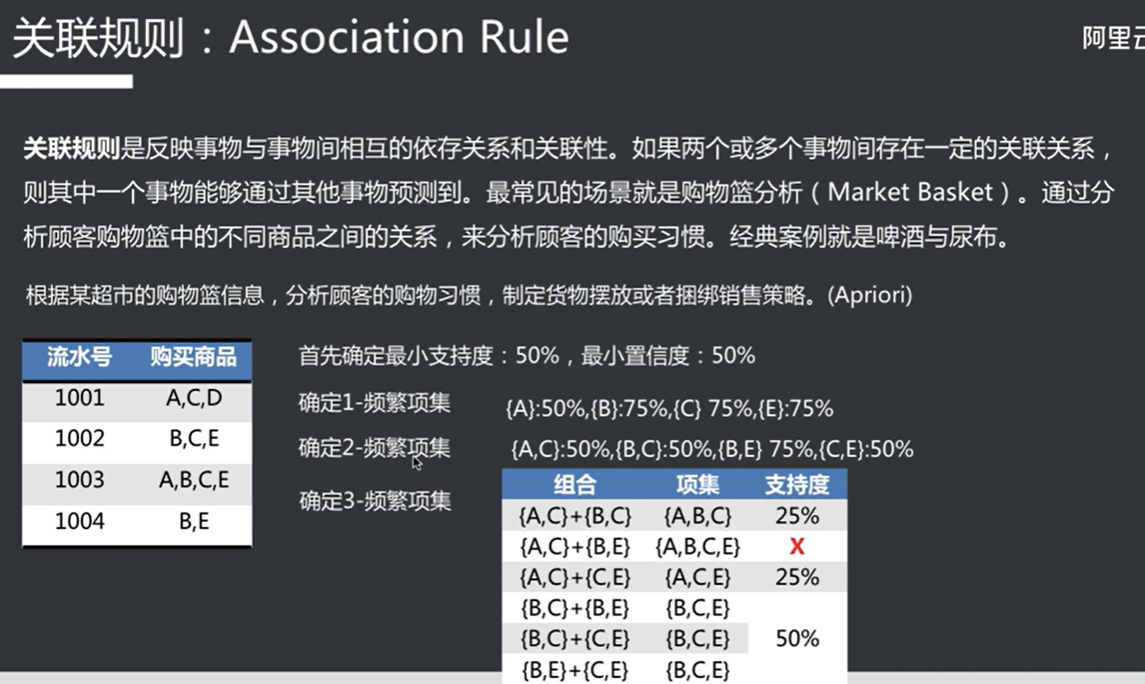
关联规则
支持度就是这个集合在样本中占的比例,置信度就是所占比例是否具有收录到项集中的意义(超过置信度才收录)
注意下一集合是由上层集合推导出来的,而不是遍历所有集合
其他算法
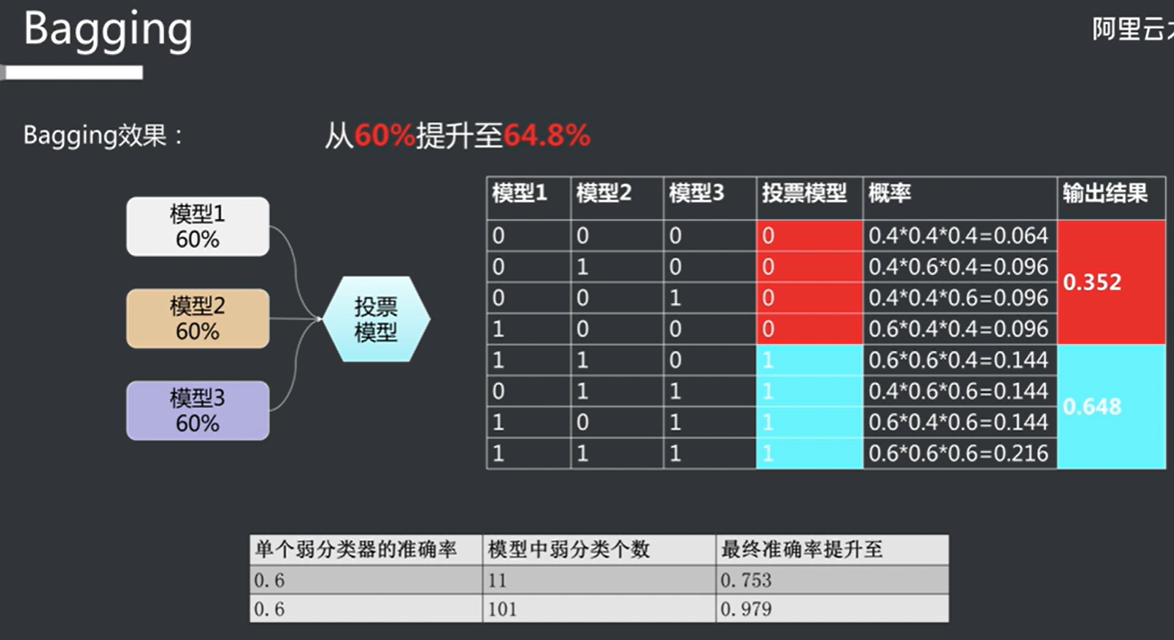
投票模型
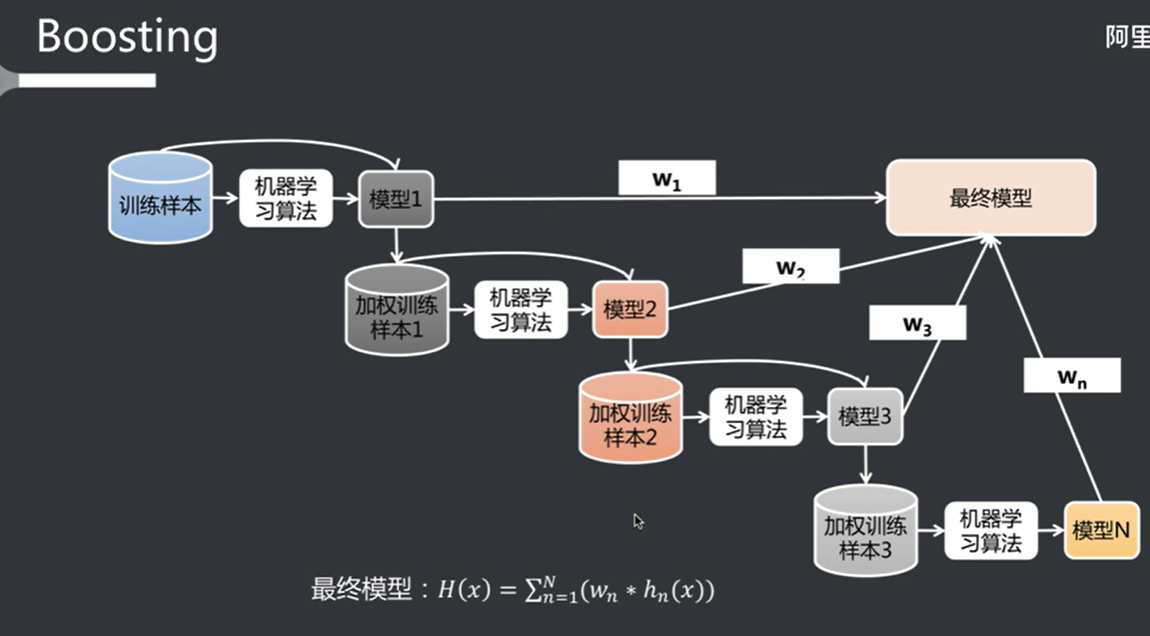
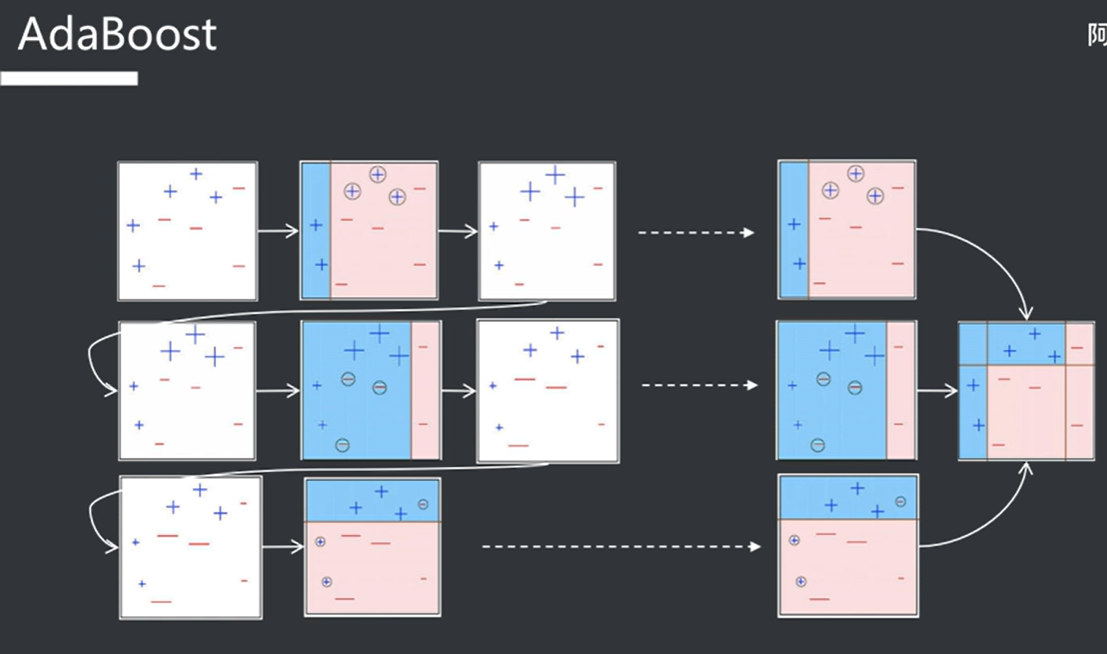
错误权重叠加迭代模型
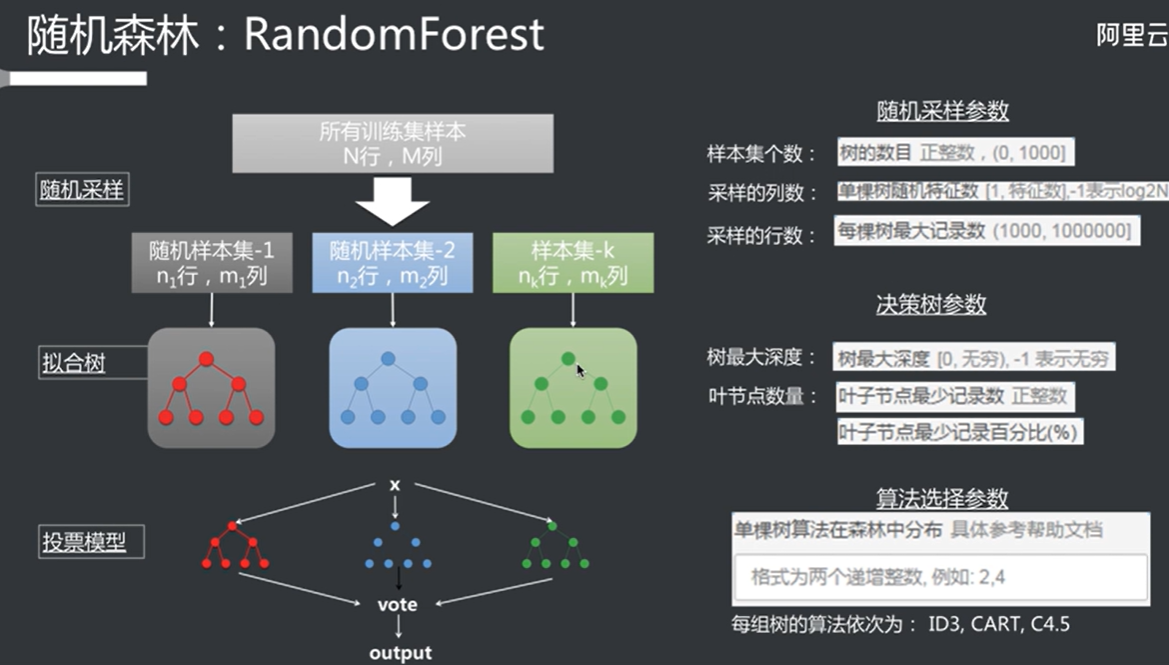
随机森林
深度学习
增强学习
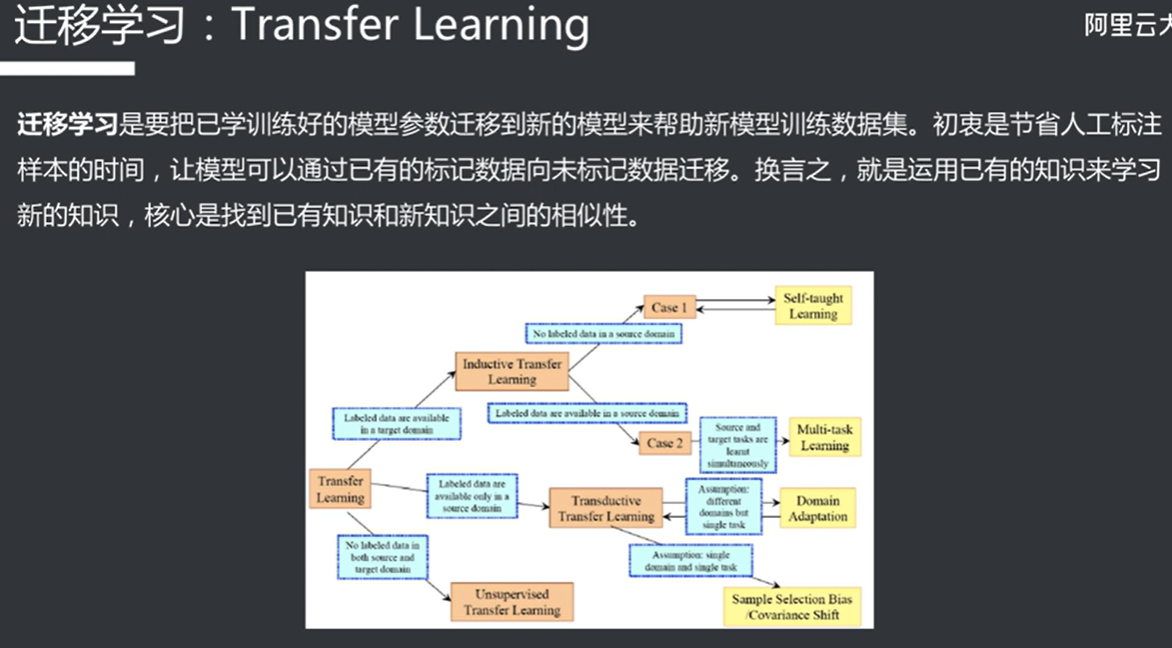
迁移学习 (增强了泛用性?
课程链接 所有课程内容均来自阿里云:
1 2 https://edu.aliyun.com/course/313926 https://developer.aliyun.com/learning/roadmap/ai